新课程理念下的教学是师生交往、积极互动、共同发展的过程，课堂作为师生学习生活的主要场所，应该是丰富多彩，充满活力的。身为数学教师，有必要重新审视自己的课堂教学，从生命的高度出发，努力构建一个动态发展的数学课堂。

一、开发动态、生长的个性化课程。

当课程由“专制”走向民主，由封闭走向开放，由专家型制走向教师开发，由学科内容走向学生经验的时候，课程就不只是“文本课程”（教学计划、教学大纲、教科书等），而更是“体验课程”（被教师与学生实实在在地体验到、感受到、领悟到、思考到的课程）。由此，教师和学生也由被动的接受者转变为课程有机的构成部分，成为课程的创造者和主体。

1.就课程内容而言，教师可以通过自身的解读，对教科书给定的内容进行自主设计、选择、开发、实施和评价，使之转化为“自己的课程”。

2.就课程的动态性建构而言，教师必须以强烈的课程资源意识主动建构与社会、世界以及学生日常生活的广泛联系。

3.就教学设计而言，必须留有充分的探索空间。传统“教师本位”的教学设计讲究教学方案的具体、详实，对每一个细节、每一个知识点甚至是教师说的每一句话都预先设定，课上照本宣科，完全忽视学生是鲜活的生命个体。数学教育发展到今天，教师们已越来越强烈地感受到，数学课堂是变幻莫测的。只要是以人为本，真正将学生作为学习主体的课堂，就必然会出现各种不同的结果，这才是真实自然，符合人性的。因此，在设计教学方案时，我们必须从大处入手，从整体上把握教学结构。

如小学数学第七册《三角形面积的计算》这一课，教材将学生的实践操作分为两个实验，即分和合。对于每一部分的操作，教参也提出了注意要点。如：将两个完全一样的三角形拼成平行四边形的时候，要注意教师的示范，让学生理解旋转和平移等概念。如果照此设计，课堂教学肯定是井井有条，层次分明，结构严谨。然而，这样的课堂，也必将扼制学生探索的积极性和创新能力。因此，教师大胆改革教材，将之设计成一堂具有高度开放性的课。

（1） 学习准备

复习正方形、长方形、平行四边形的面积计算，回忆平行四边形面积公式的推导。

（2） 实践探索

a 提出问题 平行四边形面积公式的推导，对于我们学习三角形面积计算有什么启发？鼓励学生大胆猜测。

B 实践操作 请同学们利用课前准备的长方形、正方形、平行四边形以及三角形等材料自己去探索研究。

C 交流汇报

（3）实际应用

以上设计，给学生的自主探索留下了充分的时间和空间，可以最大限度的发挥学生学习的主动性和积极性。

二、构建动态、发展的教学过程。

学习离不开人的积极参与，离不开认识主体的活动。知识属于人的认识范畴，是人在社会实践中形成并得到检验的。从这个意义上来讲，“知识”更像动词（即知识乃是一种“探究的活动”），而不是名词（即知识是绝对的，不变的结论）。课堂教学过程，是师生互教互学、相互影响的过程，是一个动态的、发展的过程。教师作为学生发展的引导者和促进者，在教学中要采用多种教学手段，调动每个学生的积极性，挖掘每个学生的潜能，发展每个学生的个性。下面就结合《三角形面积的计算》的教学过程谈谈体会：

1、注重实践探索，使教学更具体验性。

数学教学是数学活动的教学。瑞士教育家皮亚杰说过：“在逻辑——数学领域，儿童只对那些亲自创造的事物才能真正理解。”这堂课中，教师为学生的自主探索提供了充分的感性材料，提供了开放的时间与空间，以学生原有的生活经验为知识背景，在学生猜测的基础上，组织他们利用课前准备的材料自己去尝试、发现、体验和感悟，让学生经历对三角形面积公式推导的探索、发现和证明的完整过程。通过学生多种感官密切配合，协调行动，让学生真正体会和理解了三角形面积计算的方法，从而实现了教、学、做合一。

2、注重自我感悟，使教学更具发展性。

英国物理化学家和思想家波兰尼在《人的研究》中将知识分为显性知识（可表达的知识）和隐性知识（只能意会的知识）。两者的关系可用知识的冰山模型来描述：

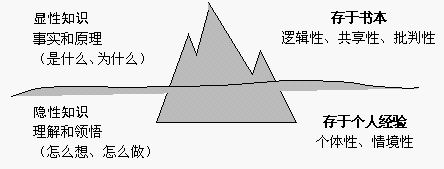
从中我们发现，我们所学到的比我们所能表达的要多的多。目前，新课程把教学目标定位于知识和技能，过程和方法，情感、态度和价值观三个维度，充分表明教学具有很大的发展性。在自主探索的过程中，每个学生都形成了自己独特的心理感受。除了与三角形面积计算有关的知识与技能的获得，还包括学习策略和方法的获得，以及情感、态度和价值观的体验。对此，教师都给予了充分的尊重和关注，促进了学生在学习中的和谐发展。

3、注重多向交流，使教学更具共享性。

课堂上生生、师生之间的交流与合作，是体现学生主体性的一个重要标志，也是形成信息多向交流和反馈的新型课堂教学结构的重要活动方式。已有的认知结构是学生学习的出发点，每个学生总是在自己已有的经验基础上以自己独特的认知方式进行学习的。因此，尊重学生的个性，在独立探究的基础上，加强学生与学生之间的交流与合作，既可以使学生学习从多角度看待问题，也可以使学生通过对比完善自己的想法，提升自己的认识，丰富自己的认知方式。即便是学生不解的地方，也要先让其他学生谈自己的看法，用学生自己思考问题的方式、学生的语言帮助其他学生。在交流汇报这一环节，充分重视学生的实践成果，提供学生充分展示自己思维的空间，让学生畅所欲言，将自己的所得通过语言表述以及演示（粘贴在磁性黑板上）展示给大家，让全班一起分享各自的想法和情感。同时，教师及时引导学生对发现进行归纳与整理，促进知识的建构。合作与交流，可以使资源充分共享，使每个学生都体验到成功的喜悦。

教学片段

师：经过积极的动脑、动手以及与小伙伴的交流、讨论，大家肯定有了许多的发现，下面我们一起来分享大家的发现。

生1：一个平行四边形沿对角可以剪成两个完全一样的三角形。

师：你怎么知道完全一样呢？

生1：（演示）可以这样重合在一起。

生2：一个长方形也可以剪成两个完全一样的三角形。

生3：两个完全一样的三角形可以拼成一个平行四边形。

师：怎么拼？

生3：先重合，再把其中一个向上打开拼到旁边。

生4：我是直接将两条相等的边拼在一起。

生5：我用两个完全一样的直角三角形通过剪、移，拼成了一个长方形。

生6：我用两个完全一样的直角三角形通过剪、移，拼成了一个正方形。

师：从生6的演示中，你还发现了什么？

生7：生6剪出来的两个三角形不仅是直角三角形，还是等腰三角形。

师：观察的真仔细！必须是两个完全一样的等腰直角三角形才能拼成一个正方形。

生8：我只用一个三角形，通过折、剪、移，也拼成了一个长方形。

师：你的想法真有创意！

……

师：刚才，大家通过剪、移、拼，将三角形与学过的长方形、正方形以及平行四边形进行了相互转化，在转化的过程中，你发现三角形的面积与这些图形的面积之间有什么联系吗？

生1：一个平行四边形可以剪成两个完全一样的三角形，因此，一个三角形的面积是平行四边形面积的一半。

生2：我发现两个等腰直角三角形拼成一个正方形后，三角形的底和高成了正方形的边长。

生3：我用两个完全一样的锐角三角形拼成了一个平行四边形，这个平行四边形的底等于三角形的底，高等于三角形的高，每个三角形的面积是拼成的平行四边形面积的一半。

生4：我把一个三角形转化成一个一个长方形后，面积没有变化。

师：仔细观察，这个三角形的底和高与转化成的长方形的长与宽之间有什么联系？

生5：长方形的长等于三角形的高，长方形的宽是三角形底的一半。

生6：我不懂，为什么长方形的宽正好是三角形底的一半呢？

生5：我来演示给你看……

生7：每个三角形的面积是与它等底等高的平行四边形面积的一半。

……

师：通过刚才的实验，你知道三角形的面积怎样计算了吗？

生：三角形的面积＝底×高÷2。

……

以上片段，是交流汇报这一环节中师生互动、生生互动的一个展示过程，这其中，教师作为学生学习的共同体，不仅充分尊重学生在解决问题过程中所表现出的不同水平，关注不同学生的体验，而且循着学生思维的起伏进行了有机的引导。在关注学生知识与能力发展的同时，也充分肯定了学生在学习过程中产生的新的发现（如上述两个完全一样的三角形拼成平行四边形的拼法以及不同见地等），促进了学生的自我发展（方法的获得、情感态度、价值观等）。

构建动态、发展的数学课堂的几点思考：

1、《数学课程标准》指出：要让不同的人在数学上得到不同的发展，要努力让不同的学生在数学学习上都获得成功。怎样的学习才是成功的学习？结合新课程的教学目标，我们认为，教师不能把眼光停留在可操作的、可表达的显性知识的考核上，而应该将关注点转向学生在课堂上的行为表现、情绪体验、过程参与、知识的获得以及交流合作等动态发展的诸多方面。

2、在新课程的标准中，有些目标是明确给出的，如：知识的目标、经历的目标等；但是，有些目标是不明确的，例如，能力的目标、方法的目标、情感、态度和价值观的目标等，这些是随着教学的发展不断生成和深化的，因此，教师必须做有心人，在实际的操作中去不断地开发、升华。

3、开放的课堂，经常会出现一些比较棘手的数学问题，在师生共同探究无果的情况下，作为教师，我们首先要敢于承认自己知识的不足，然后引导学生课后通过上网、去图书馆查阅资料以及请教他人等多种方法寻找问题的答案。

4、动态的数学课堂需要给予学生广阔的探索时空，有时学生思维正处于活跃状态，下课的铃声响了……如何妥善处理学生的探索欲望和时间安排之间的矛盾，这也是我们教育工作者需认真思考的一个问题。

参考资料：

1、《走进新课程——与课程实施者对话》

2、《知识、学习与教学——论新课程下的课堂教学》

——《课程教材教法》2003年第1期