执教者：常州市第二实验小学 孙敏

日期：2005年3月13日

班级：四（3）班

教学目标：

1．通过实际操作、尝试，将平行四边形折叠、剪切、平移，转化成学过的长方形，了解转化的这一方法在平面图形中的运用。

2．引导学生建立利用数据比较、探索新图形与已学图形之间关系的意识，从而找到平行四边形面积的计算方法，学会字母公式的表示方式。

3．在实际计算中，学会选择合适的数据求实际图形的面积。

教学过程：

一、 复习、引入。

1． 出示长方形，说说它的面积指什么？怎样求？为什么可以这样求？

2． 长方形变形成平行四边形，说说有什么变化？

二、 猜想、验证。

1． 这个平行四边形的面积有多大呢？你是怎样知道的？

2． 如果说不清楚，猜猜它的面积与谁比较接近？可以用手边的1号图形试一试。

小组活动，出示活动要求：

（1）平行四边形可以转化为什么图形？

（2）新图形与原平行四边形有什么关系？

（3）求平行四边形面积需要哪些条件？

3． 学生上台展示自己的操作过程，说说自己的思考和结论。

4． 比比，你最喜欢哪种转化和计算的方法？为什么？

5． 现在黑板上这一个平行四边形的面积你也有办法求了吗？

6． 谁能总结一下平行四边形的面积计算公式？

7． 这个公式还可以用字母表示，有谁知道吗？

8． 你有办法记得有快又对吗？

三、 练习、实践。

1． 量出手中两个平行四边形的数据，算出面积。

2． 交流度量和计算中需要注意的问题。

3． 练一练。

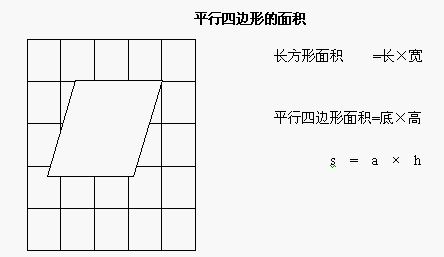
板书：

本单元教材包括五节内容：前三节分别教学平行四边形、三角形和梯形的面积计算，第四节教学土地面积单位，第五节是选学内容——组合图形的面积计算。

在上学期，学生已经认识了这些图形的名称和基本特征，在三年级，学生已学过面积的认识和长、正方形面积的计算。至本单元教学完，学生直线形的平面图形的面积就全部研究完了。

考虑到这几种图形的面积计算联系紧密，而且不论是知识还是方法都是学习圆、立体图形表面积的基础，因此，我们采用统一的结构进行教和学。在初始学习平行四边形面积计算时，我们就把目标定位在：1、把转化的意识建立起来；2、把数据的对应关系找出来，总结出计算公式；3、让学生在心中把这种方法在学习面积计算过程中的有效性确认下来。如果第一印象鲜明、清晰，学生在后继学习时就能自觉的采用这一转化的思维方法，主动的搜索需要的信息，寻求出新图形的面积计算方法，同时对图形的观察、比较、抽象等能力都能得到较好的发展。而且能对平面图形的面积和相互之间的关系建立整体的认识，融会贯通，相互证明， 灵活运用。

本节课，我们的教学重点是转化过程的理解。

难点是转化后图形与原图形各部分关系的理解和运用。因此，我们在学习过程着重处理这样几个环节：

1．动手操作，增强直观体验。

每个学生手中一个平行四边形，学生会根据各自不同的生活经验和理解，

进行自己的处理，有的学生会试图画格子，数面积单位的个数；有的学生会折，即使是无意识的折也会发现能转化成其他图形；有的学生会剪、拼，成为比较好说、好用的长方形。这一过程，学生自己动起来了，还可以看到身边同学的操作，相互启发，体验转化的过程，看到转化的结果，也比较有成就感。

2．观察转化，启发学生思维。

新的图形出来了，学生只会说可以长乘宽，但总不能每次都折、剪、量，

如何将方法推广，实用起来？这个过程学生往往并不重视，也不会主动探索。因此，我们要把这个过程夸大，由个别学生带动其他同学一起来观察，一起来思考，语言上互相提示，思维上互相激发，争取做到人人参与、人人清晰。

3．探究关系，发现计算公式。

各种转化的办法，九九归一，都是同一方法，最后都可以归纳成同一个公式。学生的能力有差异，有的学生比较敏感，知识基础较扎实，发现就比较快，对公式的记忆也是建立在对形象的理解上，但还会有部分学生只看到一个结果，因此，我们对公式的处理不能简单化，要有一个从理解到符号化的过程，花一点力气，请学生比一比，用自己的方法记一记，再抽象成字母公式，，到实际中去运用。

课后反思：

1．引入环节，由长方形的拖动变成平行四边形，教师的问题是：什么变了？什么没变？比较难，学生对周长和面积的变化说不清楚，也就产生退缩情绪，不敢发言。学生心理的障碍，也就造成课堂气氛的障碍。整个一节课，学生有些不知如何下手，不止如何表达，不止如何确定的困难。

2．自主探索的阶段，一下子出现三个问题，学生只有能力解决第一层面的问题，二、三两个问题不知道是什么意思，也就没有主动涉及，没有产生讨论。三个要求在第一节课同时出现，好像要求过高了，高估了学生。

3．当大多数学生对折的方法没有研究过，而要他们说出转化后的图形与原有图形的关系时，学生没有能积极投入的去找、去想，而是等着，等着思维好的同学或教师的告诉。在这种情况下又给时间去研究，还是效果不理想。

重建：

1． 开头不以拖动、变形为引入，而是在适当的时候作为开放练习出现，帮助学生进一步明确底和高的确定的重要性。或者仅仅提问：现在用数格子的方法还能知道平行四边形的面积吗？我们能不能找到更简洁的帮法呢？

2． 不能降低学生思维的要求，而过度包办代替。探索过程放到小组活动中进行，要求小组长边活动，边进行必要的测量、记录，将问题落实到位。

3． 当大部分学生对同一问题都有疑问时，要考虑这一问题是否对后续学习产生影响。答案是肯定的，那么，教师就要舍得花时间和力气，组织学生用各种办法验证。比如：带着大家一起量一量，发现长度之间的关系；带着大家一起折一折，比一比，发现两倍的关系。

专家评点：

1． 活动的设计从何而来，不是说教师想安排几个活动，而是根据教学目标，我需要设置几个活动，每个活动又是如何为目标服务的。

2． 活动与活动之间要有递进，要体现出层次，这个层次不仅是知识上的，更应该是学生探索活动的层次，学生思维上的层次，学生的学习需求上的层次。